How to Read Dot Decison Tree Results

Scikit-Learn Conclusion Copse Explained

Training, Visualizing, and Making Predictions with Decision Trees

Photo by Lukasz Szmigiel on Unsplash

Decision trees are the most important elements of a Random Forest. They are capable of fitting compl eastward x data sets while assuasive the user to see how a decision was taken. While searching the web I was unable to detect 1 clear article that could easily depict them, so here I am writing almost what I have learned so far. It's of import to notation, a single determination tree is non a very proficient predictor; however, past creating an ensemble of them (a forest) and collecting their predictions, i of the about powerful machine learning tools can be obtained — the so called Random Woods.

Make sure you have installed pandas and scikit-acquire on your auto. If you haven't, you can learn how to do so hither.

A Scikit-Learn Decision Tree

Allow's outset by creating decision tree using the iris blossom data set. The iris information set contains four features, three classes of flowers, and 150 samples.

Features: sepal length (cm), sepal width (cm), petal length (cm), petal width (cm)

Classes: setosa, versicolor, virginica

Numerically, setosa flowers are identified by goose egg, versicolor by 1, and virginica by two.

For simplicity, nosotros will train our decision tree using all features and setting the depth to two.

Visualizing The Decision Tree

Of grade we nonetheless do non know how this tree classifies samples, so let's visualize this tree by first creating a dot file using Scikit-Acquire export_graphviz module and so processing it with graphviz.

This will create a file named tree.dot that needs to exist candy on graphviz . Here is a YouTube tutorial that shows you lot how to process such a file with graphviz. The end issue should be similar to the one shown in Figure-i; however, a different tree might sprout even if the training data is the same!

Figure-i) Our decision tree: In this case, nodes are colored in white, while leaves are colored in orange, greenish, and purple. More nearly leaves and nodes later.

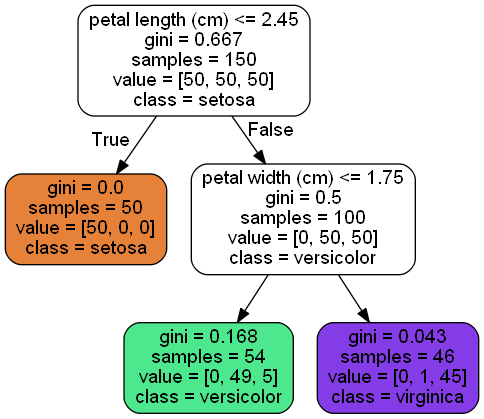
A single decision tree is the classic example of a type of classifier known as a white box. The predictions made past a white box classifier can easily exist understood. Here is an excellent commodity almost black and white box classifiers.

Understanding the Contents of a Node

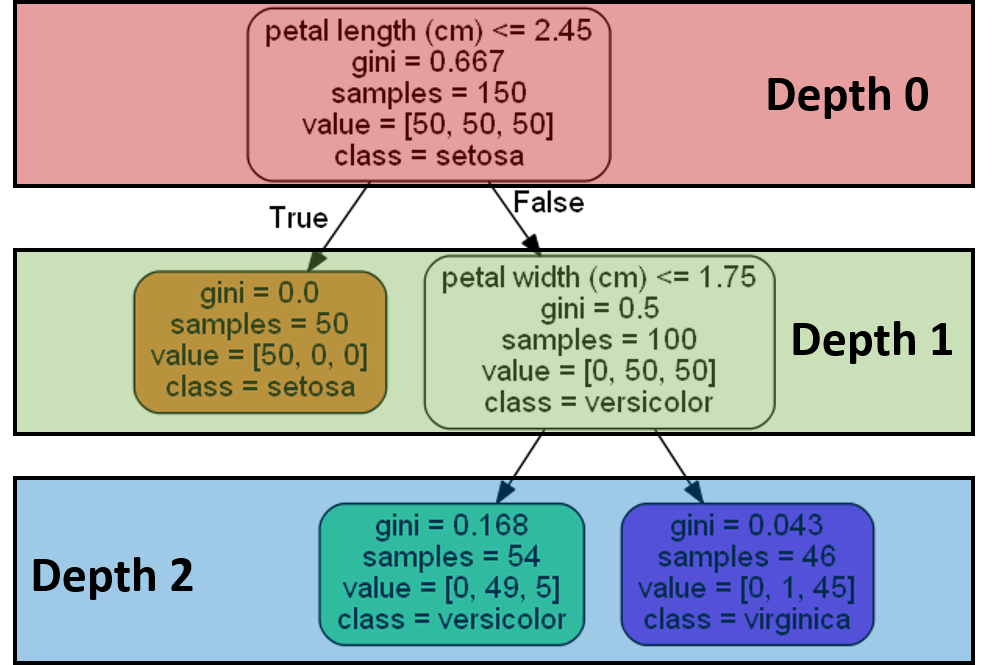
In Figure-1, yous can encounter that each box contains several characteristics. Permit'due south get-go past describing the content of the top near node, most commonly referred to every bit the root node. The root node is at a depth of zero, see Figure-2. A node is a bespeak along the decision tree where a question is asked. This action divides the data into smaller subsets.

Effigy-ii) The depth of the tree: The light colored boxes illustrate the depth of the tree. The root node is located at a depth of aught.

petal length (cm) <=2.45: The first question the determination tree ask is if the petal length is less than 2.45. Based on the result, it either follows the true or the false path.

gini = 0.667: The gini score is a metric that quantifies the purity of the node/leaf (more than near leaves in a bit). A gini score greater than zero implies that samples contained inside that node vest to different classes. A gini score of aught means that the node is pure, that within that node simply a single class of samples exist. You can detect out more than nigh impurity measures here. Observe that we take a gini score greater than nothing; therefore, nosotros know that the samples independent within the root node belong to dissimilar classes.

samples = 150: Since the iris bloom data set contains 150 samples, this value is prepare to 150.

value = [50, 50, 50]: The value list tells you lot how many samples at the given node fall into each category. The first element of the list shows the number of samples that vest to the setosa grade, the second chemical element of the list shows the number of samples that belong to the versicolor form, and the third element in the list shows the number of samples that belong to the virginica class. Detect how this node is not a pure i since different types of classes are contained inside the same node. We knew this already from the gini score, but it'south nice to actually see information technology.

grade = setosa: The form value shows the prediction a given node will make and information technology can be determined from the value list. Whichever class occurs the virtually within the node will be selected equally the course value. If the decision tree were to terminate at the root node, information technology would predict that all 150 samples belonged to the setosa class. Of form this makes no sense, since at that place is an equal number of samples for each class. It seems to me that the decision tree is programmed to cull the first class on the list if at that place is an equal number of samples for each form.

Understanding How a Tree Makes a Split

To decide which feature to employ to make the commencement split — that is, to make the root node — the algorithm chooses a feature and makes a split up. It and then looks at the subsets and measures their impurity using the gini score. It does this for multiple thresholds and determines that the best split up for the given feature is the i that produces the purest subsets. This is repeated for all the features in the preparation set. Ultimately, the root node is adamant by the feature that produces a carve up with purest subsets. Once the root node is decided, the tree is grown to a depth of one. The same process is repeated for the other nodes in the tree.

Understanding How a Tree Will Brand a Prediction

Suppose nosotros have a flower with petal_length = 1 and petal_width = 3. If nosotros follow the logic of the decision tree shown on Effigy-ane, we will see that nosotros will finish up in the orange box. In Figure-1, if the question a node asks turns out to be true (false), we volition move to the left (right). The orange box is at a depth of one, see Figure-2. Since at that place is nix growing out of this box, we will refer to it as a leaf node. Notice the resemblance this has to an actual tree, run across Figure-3. Moreover, note that the gini score is zero — which makes it a pure leaf. The total number of samples is 50. Out of the 50 samples that end up on the orange leaf node, we can see that all of them belong to the setosa class, see the value list for this leaf. Therefore, the tree will predict that the sample is a setosa bloom.

Figure-three) Real tree vs Decision Tree Similarity: The tree on the left is inverted to illustrate how a tree grows from its root and ends at its leaves. Seeing the decision tree on the right should make this analogy more clear.

Let us selection a more interesting sample. For example, petal_length = 2.60 and petal_width = 1.2 . We start at the root node which asks whether the petal length is less than 2.45. This is false; therefore nosotros move to the internal node on the right, where the gini score is 0.v and the total number of samples is 100. This internal node at a depth of one will enquire the question "Is the petal width less than 1.75?" In our case, this is true, so we move to the left and end up in the green colored leaf node which is at a depth of 2. The decision tree will predict that this sample is a versicolor flower. You can see that this is most likely the case considering 49 out of the 54 samples that end up in the dark-green leaf node were versicolor flowers, see the value list for this leaf.

Making a Prediction On a New Samples Using a Trained Tree

Now that nosotros know how our decision tree works, allow us brand predictions. The input should be in a list and ordered equally [sepal length, sepal width, petal length, petal width] where the sepal length and sepal width wont affect the predictions made by the decision tree shown in Figure-i; therefore, nosotros volition can assign them an arbitrary value.

The output should be:

This is exactly what we predicted by following the Decision Tree logic.

Scikit-Learn Conclusion Tree Parameters

If you take a look at the parameters the DecisionTreeClassifier can accept, you lot might exist surprised and so, permit'southward look at some of them.

criterion : This parameter determines how the impurity of a split will exist measured. The default value is "gini" merely you tin can also apply "entropy" as a metric for impurity.

splitter: This is how the decision tree searches the features for a split. The default value is set to "all-time". That is, for each node, the algorithm considers all the features and chooses the best split. If you determine to set the splitter parameter to "random," so a random subset of features will be considered. The split will then be made past the all-time feature within the random subset. The size of the random subset is determined by the max_features parameter. This is partly where a Random Forest gets its proper name.

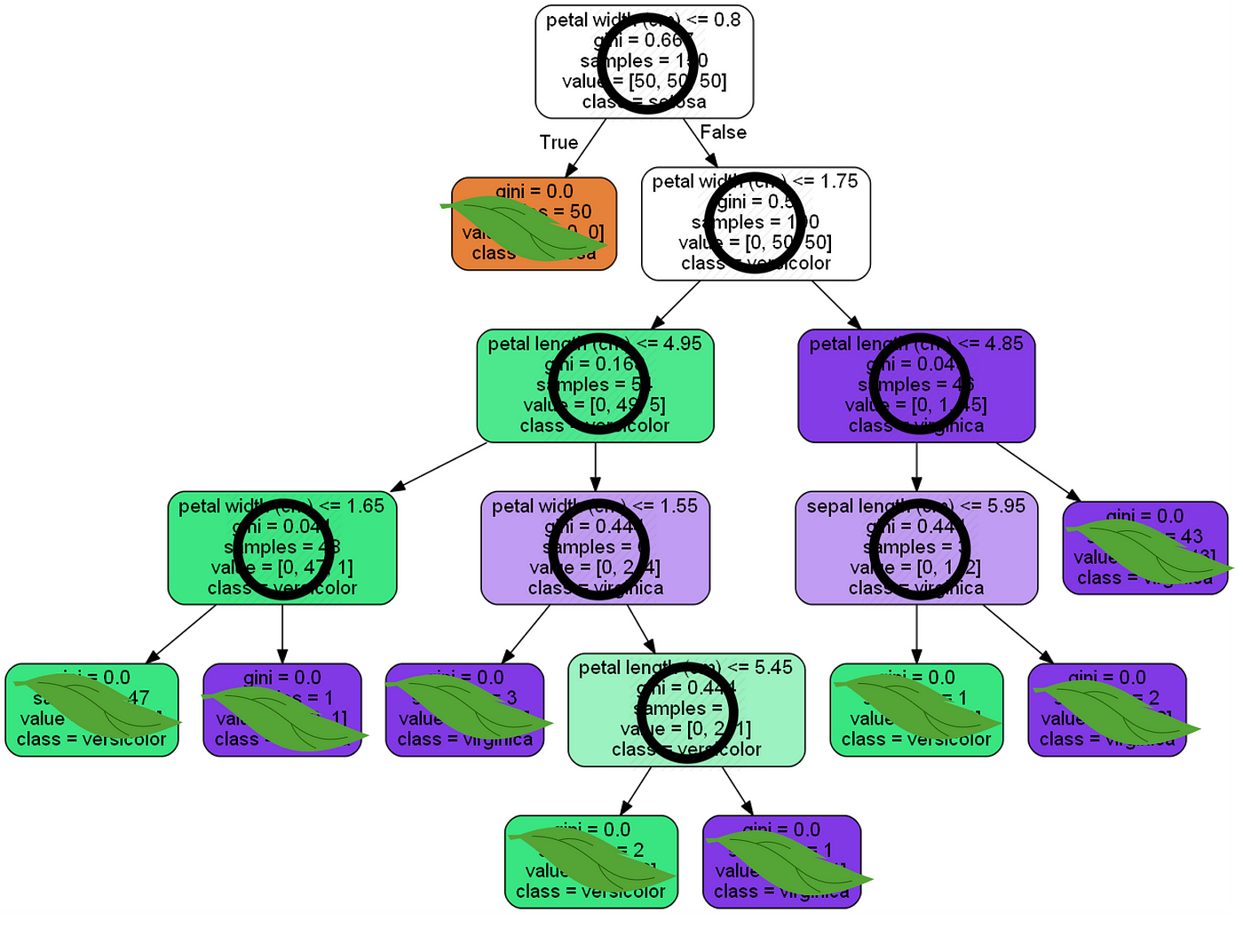
max_depth: This determines the maximum depth of the tree. In our case, we apply a depth of 2 to brand our decision tree. The default value is set to none. This will often result in over-fitted decision trees. The depth parameter is ane of the ways in which we tin can regularize the tree, or limit the style it grows to foreclose over-fitting. In Figure-iv, you tin see what happens if you don't set the depth of the tree — pure madness!

Figure-4) A fully grown Decision Tree: In the tree shown higher up, none of the parameters were set. The tree grows to a fully to a depth of five. At that place are eight nodes and ix leaves. Not limiting the growth of a determination tree may atomic number 82 to over-fitting.

min_samples_split: The minimum number of samples a node must contain in club to consider splitting. The default value is two. You lot can employ this parameter to regularize your tree.

min_samples_leaf: The minimum number of samples needed to be considered a leaf node. The default value is set to one. Use this parameter to limit the growth of the tree.

max_features: The number of features to consider when looking for the best split up. If this value is not set, the determination tree volition consider all features bachelor to make the best dissever. Depending on your application, it'south often a proficient idea to tune this parameter. Here is an article that recommends how to fix max_features.

For syntax purposes, lets set some of these parameters:

Closing Remarks

At present y'all know how create a decision tree using Scikit-acquire. More importantly, you lot should be able to visualize it and understand how it classifies samples. Information technology's of import to note that one needs to limit the freedom of a determination tree. In that location are several parameters that can regularized a tree. By default, the max_depth is set to none. Therefore, a tree will grow fully, which often results in over-plumbing fixtures. Moreover, a single determination tree is not a very powerful predictor.

The existent power of decision trees unfolds more so when cultivating many of them — while limiting the way they grow — and collecting their individual predictions to course a terminal decision. In other words, you grow a forest, and if your forest is random in nature, using the concept of bagging and with splitter = "random", we telephone call this a Random Forest. Many of the parameters used in Scikit-Learn Random Woods are the same ones explained in this article. So it's a good thought to understand what a single decision tree is and how information technology works, earlier moving on to using the big guns.

You can detect me in LinkedIn or visit my personal web log.

parkerunuter.blogspot.com

Source: https://towardsdatascience.com/scikit-learn-decision-trees-explained-803f3812290d

Share this post